Analytic Hierarchy Process (AHP) is a structured technique for organizing and analyzing complex decisions.

I’m blogging after a very long time now and it’s for a good reason actually - I’m planning to document all my optimization learning, which is a new area that I have been exploring for sometime now.

Optimization in my view let’s you make good decisions and beauty about the math behind all the optimization algos is that you end up with a result which will help you take an informed decision.

Multiple-criteria decision analysis

This analysis in simple word helps you make decision based on a lot of real world criterias! Comes under the operational research discipline

Analytic Hierarchy Process(AHP)

Analytic Hierarchy Process (AHP) is a structured technique for organizing and analyzing complex decisions.

We all make decisions in every point of life, look at pros and cons and come up with the best decision that suits the need. AHP works in a simillar way,

Wide range of applications exists:

• Selecting a car for purchasing
• Deciding upon a place to visit for vacation
• Deciding upon an MBA program after graduation

AHP algorithm is basically composed of two steps:

1. Determine the relative weights of the decision criteria
2. Determine the relative rankings (priorities) of alternatives

Let’s take example of Car selection,

Objective: Selecting the best car Criteria: Style, Reliability, Fuel-economy Cost? Options: Civic Coupe, Saturn Coupe, Ford Escort, Mazda Miata

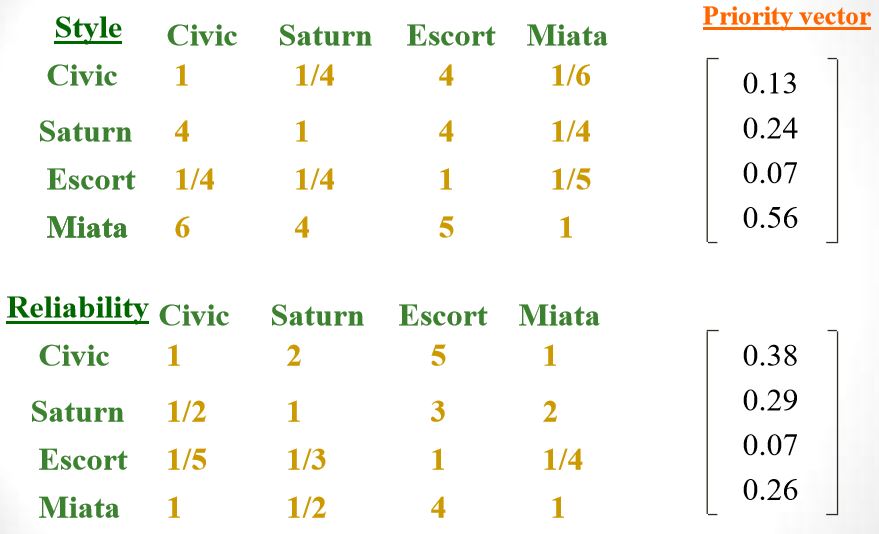
Ranking of criteria

We fill the matrix where we enter values based on the importance of the feature (liquor scale)

To find the ranking of priorities, namely the Eigen Vector X: 1) Normalize the column entries by dividing each entry by the sum of the column 2) Take the overall row averages.

These are the criteria weights where if selecting a new car (1.0) = Style (.32), Reliability (.56), Fuel Economy (.12)

Checking for consistency

Consistency Ratio (CR) to measure how consistent the judgments have been relative to large samples of purely random judgments. AHP evaluations are based on the aasumption that the decision maker is rational, i.e., if A is preferred to B and B is preferred to C, then A is preferred to C

If the CR is greater than 0.1 the judgments are untrustworthy because they are too close for comfort to randomness and the exercise is valueless or must be repeated.

Ranking alternatives to find the proroty vector

Since fuel economy is a quantitative measure, fuel consumption ratios can be used to determine the relative ranking of alternatives

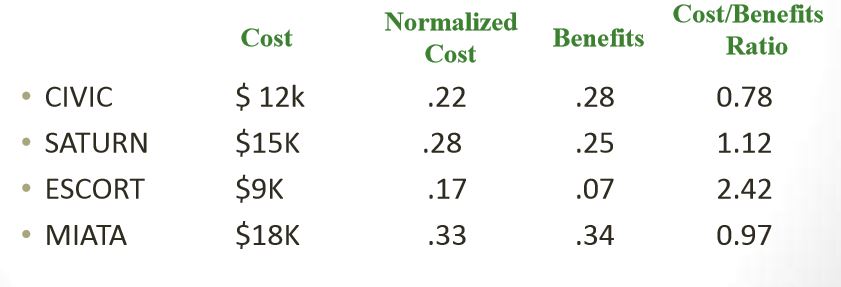
Adding “cost” as a a new criterion is very difficult in AHP. A new column and a new row will be added in the evaluation matrix. However, whole evaluation should be repeated since addition of a new criterion might affect the relative importance of other criteria as well! Instead one may think of normalizing the costs directly and calculate the cost/benefit ratio for comparing alternatives!

To be continued… (There are more techniques to document under this topic)

Views expressed are my own and are not linked to my affiliations in any manner.